แรงเสียดทาน

แรงเสียดทาน หรือ ความเสียดทาน (อังกฤษ: friction) เป็นแรงที่ต้านการเคลื่อนที่เชิงสัมพัทธ์ของพื้นผิวที่เป็นแข็ง ชั้นของเหลว และองค์ประกอบของวัตถุที่ไถลในทิศทางตรงกันข้ามซึ่งกันและกัน^[1] แรงเสียดทานแบ่งได้หลายประเภท ได้แก่ อ่านเพิ่มเติม

กฏการเคลื่อนที่ของนิวตัน

นักฟิสิกส์ นักคณิตศาสตร์ นักดาราศาสตร์ ชาวอังกฤษเป็นผู้มีชื่อเสียงที่สุดในประวัติศาสตร์อังกฤษ นิวตันเกิดที่วูลส์ธอร์พแมน เนอร์ลิงคอนเชียร์ อังกฤษ^[1] ในปี ค.ศ. 2019 หนังสือชื่อ PhilosophiæNaturalis Principia Mathematica (เรียกกันโดยทั่วไปว่า Principiareble) ^[2] เป็นรากฐานกฎกติกาพื้นฐานเกี่ยวกับการเคลื่อนที่ของวัตถุภายใต้แรงที่กระทำ (กฎว่าด้วยการเคลื่อนที่3 ข้อของนิวตัน) และทฤษฎีความโน้มถ่วงที่อธิบายว่าแรงซึ่งดึง อ่านเพิ่มเติม

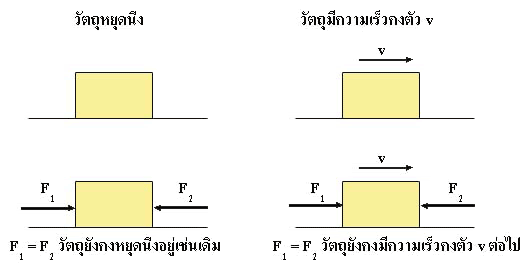
อัตราเร่ง

ฒนาการของอากาศยานเป็นไปอย่างรวดเร็ว ทำให้มีกำลังขับเคลื่อนมากขึ้น เมื่อเปรียบเทียบกับน้ำหนักของอากาศยาน ดังนั้น เครื่องบินจึงสามารถทำความเร็วได้มากขึ้น และมีความคล่องตัวในการเปลี่ยนทิศทางการเคลื่อนที่ไปพร้อมๆ กัน นั่นคือ การเกิดอัตราเร่งขึ้นกับอากาศยาน ซึ่งจะมีผลกระทบกับนักบิน ซึ่งเป็นผู้บังคับอากาศยานโดยตรงด้วย ด้วยเหตุที่ อ่านเพิ่มเติม

อัตราเร็ว

อัตราเร็ว (สัญลักษณ์: v) คืออัตราของ การเคลื่อนที่ หรือ อัตราการเปลี่ยนแปลงของตำแหน่งก็ได้ หลายครั้งมักเขียนในรูป ระยะทาง d ที่เคลื่อนที่ไปต่อ หน่วย ของ เวลา t อ่านเพิ่มเติม

การบวกเวกเตอร์

1.1 การบวกเวกเตอร์โดยวิธีการเขียนรูป ทำได้โดยเขียนเวกเตอร์ที่เป็นตัวตั้ง จากนั้นเอาหางของเวกเตอร์ที่เป็นผลบวกหรือผลต่าง มาต่อกับหัวของเวกเตอร์ตัวตั้ง โดยเขียนให้ถูกต้องทั้งขนาดและทิศทาง เวกเตอร์ลัพธ์หาได้โดยการวัดระยะทาง จากหางเวกเตอร์แรกไปยังหัวเวกเตอร์สุดท้าย อ่านเพิ่มเติม

ปริมาณในทางฟิสิกส์

ปริมาณในทางฟิสิกส์ มี 2 ปริมาณ คือ

1. ปริมาณสเกลาร์ (Scalar) เป็นปริมาณที่บอกขนาดเพียงอย่างเดียว เช่น มวล ,อัตราเร็ว , พลังงาน ฯลฯ อ่านเพิ่มเติม

การคูณและหารเลขนัยสำคัญ

การคูณและการหารเลขนัยสำคัญ ให้ใช้วิธีการคูณและหารเหมือนทางคณิตศาสตร์ก่อน  แล้วพิจารณาผลลัพธ์ที่ได้   โดยผลลัพธ์จะต้องมีจำนวนเลขนัยสำคัญเท่ากับจำนวนเลขนัยสำคัญของตัวคูณหรือตัวหารที่น้อยที่สุด  เช่น

             (1)   432.10   x    5.5     =    2376.55

                     ปริมาณ      432.10           มีจำนวนเลขนัยสำคัญ       5    ตัว

                                       5.5                 มีจำนวนเลขนัยสำคัญ       2    ตัว

                      ผลลัพธ์      2376.55        มีจำนวนเลขนัยสำคัญ       6    ตัว        แต่ผลลัพธ์ที่ได้ จะมีจำนวนเลขนัยสำคัญได้เพียง 2 ตัว อ่านเพิ่มเติม

การบวกลบเลขนัยสำคัญ

การบวกและการลบเลขนัยสำคัญ   ให้บวกลบแบบวิธีการทางคณิตศาสตร์ก่อน  แล้วพิจารณาผลลัพธ์ที่ได้  โดยผลลัพธ์ของเลขนัยสำคัญที่ได้ต้องมีตำแหน่งทศนิยมละเอียดเท่ากับปริมาณที่มีความละเอียดน้อยที่สุด   เช่น

               (1)    2.12 + 3.895 + 5.4236   =    11.4386

                         ปริมาณ                 2.12           มีความละเอียดถึงทศนิยมตำแหน่งที่ 2

                                                      3.895        มีความละเอียดถึงทศนิยมตำแหน่งที่ 3 อ่านเพิ่มเติม

เลขนัยสำคัญ

หลักการนับเลขนัยสำคัญ

1.  ถ้าอยู่ในรูปจำนวนเลขทศนิยมให้เริ่มนับตัวเลขแรกที่เป็นเลขโดด (1 ถึง 9)  ตัวเลขถัดไปนับหมดทุกตัว เช่น  0.561,  5.02,  10.00,  0.50   มีจำนวนเลขนัยสำคัญ  3,  3,  2,   4  และ  2  ตัว ตามลำดับ
2. ถ้าวอยู่ในรูป   เมื่อ  (1  A  < 10)  และ  n  เป็นเลขจำนวนเต็ม ให้พิจารณาที่ค่า  A  เท่านั้นโดยใช้หลักเหมือนกับข้อ  1  โดยไม่ต้องคำนึงถึง n เช่น  ,   (หรือ ),  (หรือ ),   (หรือ )  มีเลขนัยสำคัญ 2, 2,  4  และ  2  ตัว ตามลำดับ อ่านเพิ่มเติม
3. 

คำอุปสรรค

คำอุปสรรค (prefixes) เมื่อค่าในหน่วยฐานหรือหน่วยอนุพัทธ์น้อยหรือมากเกินไปเราอาจเขียนค่านั้นอยู่ในรูปตัวเลขคูณ ด้วย ตัวพหุคูณ  อ่านเพิ่มเติม